BIP32 Cheat Sheet

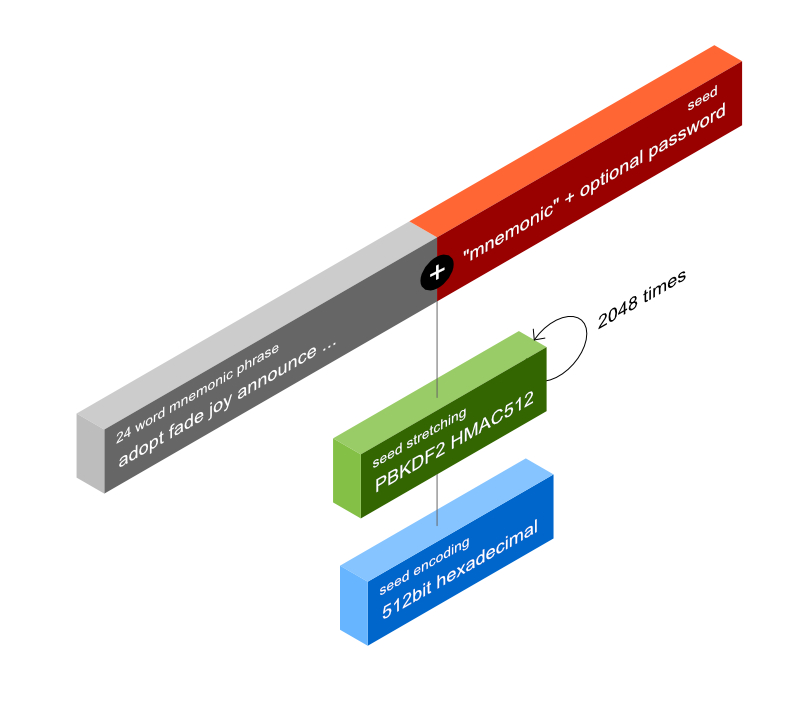
Generate the seed

Stretching the 256bit entropy from menmonic words into 512bit seed

1. Salt

   Create a salt. If no password is chosen, the salt will be comprised of the string "mnemonic"

2. Key Stretching

   Create initial PBKDF2 round by passing the entropy as the key and the salt as the data.

3. Repeat 2048 times

   Repeat this 2048 times. The entropy parameter stays the same, while the data is the xor of the current and previous result

4. Encode in hexadecimal

   Generally the seed is exported as a hex string.

Anatomy of an exteded key

An extended key is a Base58Check encoded string that encodes a few pieces of information.

1. Version Number

   4 bytes that denote weather we're encoding a public or private key. The version number is what starts an extended by with xpub or xprv. The bytes in the version number combined with the rest of the data produces the xpub/xprv in Base58 encoding.

2. Depth

   1 byte that denotes the depth.

3. Fingerprint

   4 bytes (the first 4 bytes of the SHA256 --> Ripemd160 hash of the parent key)

4. Index

   4 bytes

5. Chain Code

   32 bytes

6. Key

   33 bytes - If private key it will be prepended with a zero byte

Child Key Derivation (public, non-hardened)

A non hardened child key derivation means that we will use the parent's public key to derive the child key. It also means that the index will be at most 2_147_483_647

1. Split the derivation path into list of integers.

   This is a non-hardened path so we won't get any ' in the path (ie. m/0/0)

2. Decode parent extended key

   This will result in a key, chain code, depth, index and version number.

3. Calculate child fingerprint from parent key

   This is the first 4 bytes of the SHA256 -> RIPEMD160 hash functions.

4. Increase the depth and index

   Depth increases by 1 while index by the path number currently deriving.

5. Calculate PBKDF2 HMAC512 of the parent chain code & key + index

   The resulting 512bit number is the child key (first 256bits and the child chain code the rest 256bits)

6. Use resulting key to perform EC curve multiplication with G to compute child public key.

   This is the same point multiplication we use to derive a public key from a private key, except this time we use the parent public key to derive a child public key.

7. De-compress the parent public key into the X and Y coordinates.
8. Perform EC point addition of the P(X,Y) and the child public key.

   This step is required to get the X and Y coordinates of the resulting child key.

9. Check if the resulting X, Y coordinate fall within the curve's finite field.

   The resulting extended by is just the compressed version (just the X coordinate) of the (X,Y) point. We append 02 if the Y coordinate is even or 03 otherwise.

10. Encode resulting data with Base58Check

    The version number used will be the public one.

Child Key Derivation (private, un-hardened)

The private child key derivation is similar to the public one with a few exceptions.

1. Split the derivation path into list of integers.

   This is a non-hardened path so we won't get any ' in the path (ie. m/0/0)

2. Decode parent extended key

   This decoded key will have a 0 appended to it and we need to strip that.

3. Calculate the public key using EC multiplcation.

   This is the first 4 bytes of the SHA256 -> RIPEMD160 hash functions.

4. Compress the public key obtained in the previous step.

   Depth increases by 1 while index by the path number currently deriving.

5. Use the compressed public key from previous step to calculate the fingerprint.

   The resulting 512bit number is the child key (first 256bits and the child chain code the rest 256bits)

6. Calculate depth.

   This is the same point multiplication we use to derive a public key from a private key, except this time we use the parent public key to derive a child public key.

7. Use PBKDF2 HMAC512 to calculate child key and chaincode.

   This is the same point multiplication we use to derive a public key from a private key, except this time we use the parent public key to derive a child public key.

8. Run the resulting key through mod curve order to ensure the point falls within the finite field.
9. Encode resulting data with Base58Check

   We're using the private version number here.

Child Key Derivation (hardened)

A hardened derivation offsets the index of each path integer by 2^31. All the previous steps apply except that for both private and public derivation the resulting public or private key is calculated using the parent private key. This means that you can't derive a downstream path for a hardened path.

1. Use resulting key to perform EC curve multiplication with G to compute child public or private key.

   We're using the parent private key to perform this step as stated above. This means that if we have an extended public key and we want to derive a path like m/0' we won't be able to because we don't have access to the private key which is required in this step.

Addresses

Once we have a way to generate a tree of public keys, getting a blockchain address is only a matter of hashing or encoding it the right way.

• Bitcoin

  A bitcoin pay-to-hash address is a SHA256 -> RIPEMD160 -> Base58Check of the compressed public key.

• Ripple

  A ripple address is similarly a SHA256 -> RIPEMD160 -> Base58Check but with a different alphabet than Bitcoin. That's why addresses look different.

• Ethereum

  Ethereum addresses start from the same precursor as Bitcoin and Ripple, except we use the un-compressed public key (concatenated X and Y), take the Keccak256 hash of that and keep the last 20 bytes.